Counting over Range Predicates
This post follows on from my last post about selecting objects satisfying a range predicate, and instead looks at how to count the objects. If you can select objects, you can count them too, but it’s a simpler problem so resources can be saved with a specialised solution.
Suppose you want to count how many of the Transaction objects below satisfy complex filters, and don’t care about details about the objects themselves.
public static final class Transaction {
private final int quantity;
private final long price;
private final long timestamp;
public Transaction(int quantity, long price, long timestamp) {
this.quantity = quantity;
this.price = price;
this.timestamp = timestamp;
}
public int getQuantity() {
return quantity;
}
public long getPrice() {
return price;
}
public long getTimestamp() {
return timestamp;
}
}
Once again, this sounds like a task for a database, but imagine you don’t have one to rely on.
You might use the streams API:
transactions.stream()
.filter(transaction -> transaction.quantity >= qty && transaction.price <= price
&& transaction.timestamp >= begin && transaction.timestamp <= end)
.count();
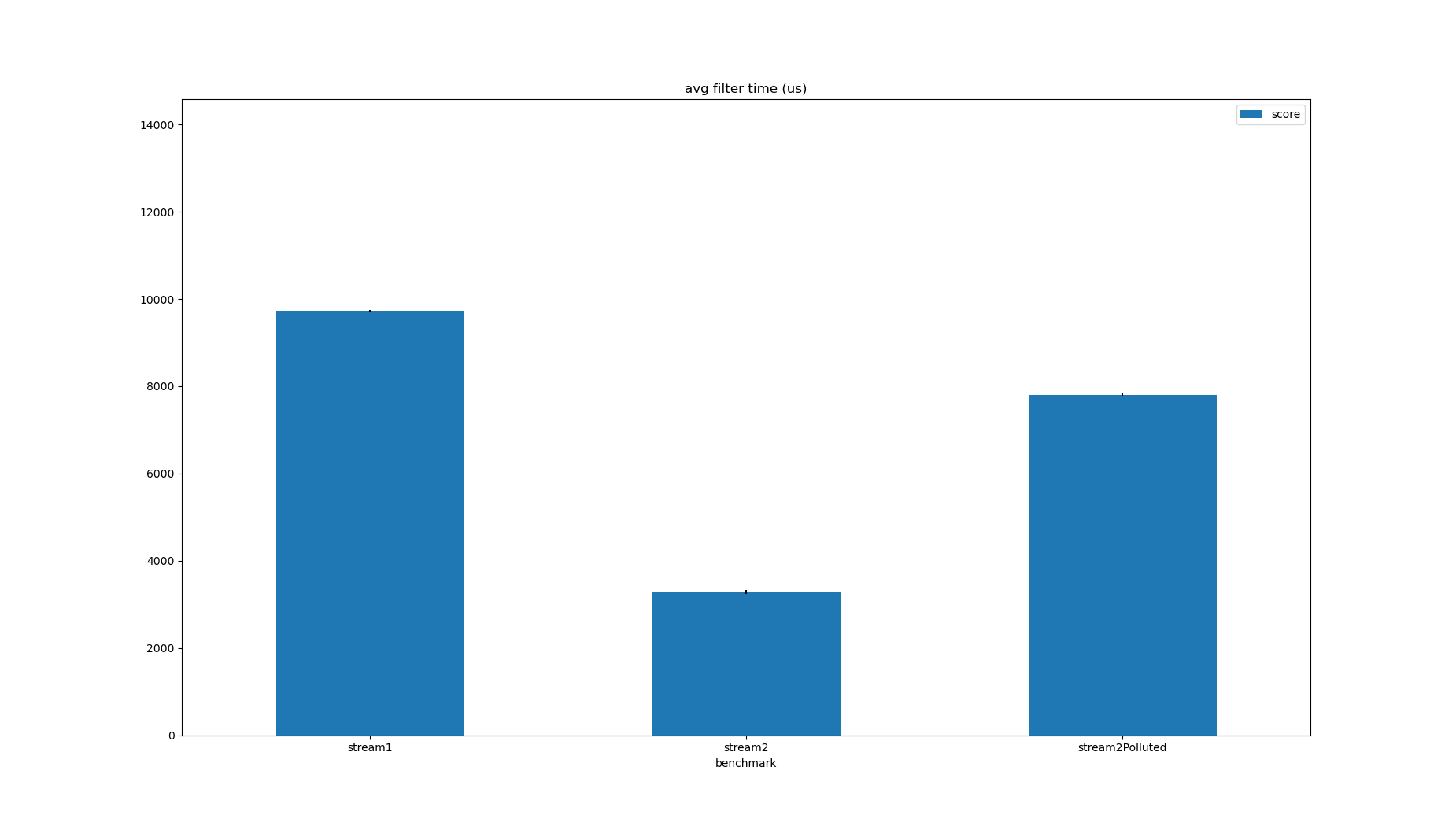
This will inspect every transaction to check if it matches the constraints, and will count the number of matches. For 1M transactions, with parameters which select about 250 transactions, this takes about 10ms on my laptop:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
It took less time to actually select the objects, which, without any knowledge of the implementation, suggests that the objects are probably selected in order to be counted. The transactions are the same as those in the previous post, and sorted by time. This means reordering the conditions to the time filter is applied first is as effective as it was last time by reducing the number of branch misses.
transactions.stream()
.filter(transaction -> transaction.timestamp >= begin && transaction.timestamp <= end
&& transaction.quantity >= qty && transaction.price <= price)
.count();
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3283.291345 | 44.566458 | us/op | 100 | 1 | 1000000 |
Something easy to ignore in a Stream API benchmark is how much better the performance is when there is only one implementation of the filter, which allows the filter to be inlined.
This makes the code in the benchmark artificially simple, when really the whole point of the API is that many filters would be used, which is a triumph of modularity over efficiency (but you should use the right tool for the job and know when such a difference matters).
Artificially polluting the filter in the benchmark setup shows how artificial the result for stream2 was:
@Setup(Level.Trial)
public void setup() {
super.setup();
transactions.stream()
.filter(transaction -> transaction.quantity < 0 && transaction.price > 1
&& transaction.timestamp >= 1 && transaction.timestamp <= Long.MAX_VALUE - 1)
.count();
transactions.stream()
.filter(transaction -> transaction.quantity < 10 && transaction.price > 1000
&& transaction.timestamp >= -1 && transaction.timestamp <= Long.MAX_VALUE - 1)
.count();
}
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3283.291345 | 44.566458 | us/op | 100 | 1 | 1000000 |
| stream2Polluted | avgt | 1 | 5 | 7801.823477 | 41.229256 | us/op | 100 | 1 | 1000000 |
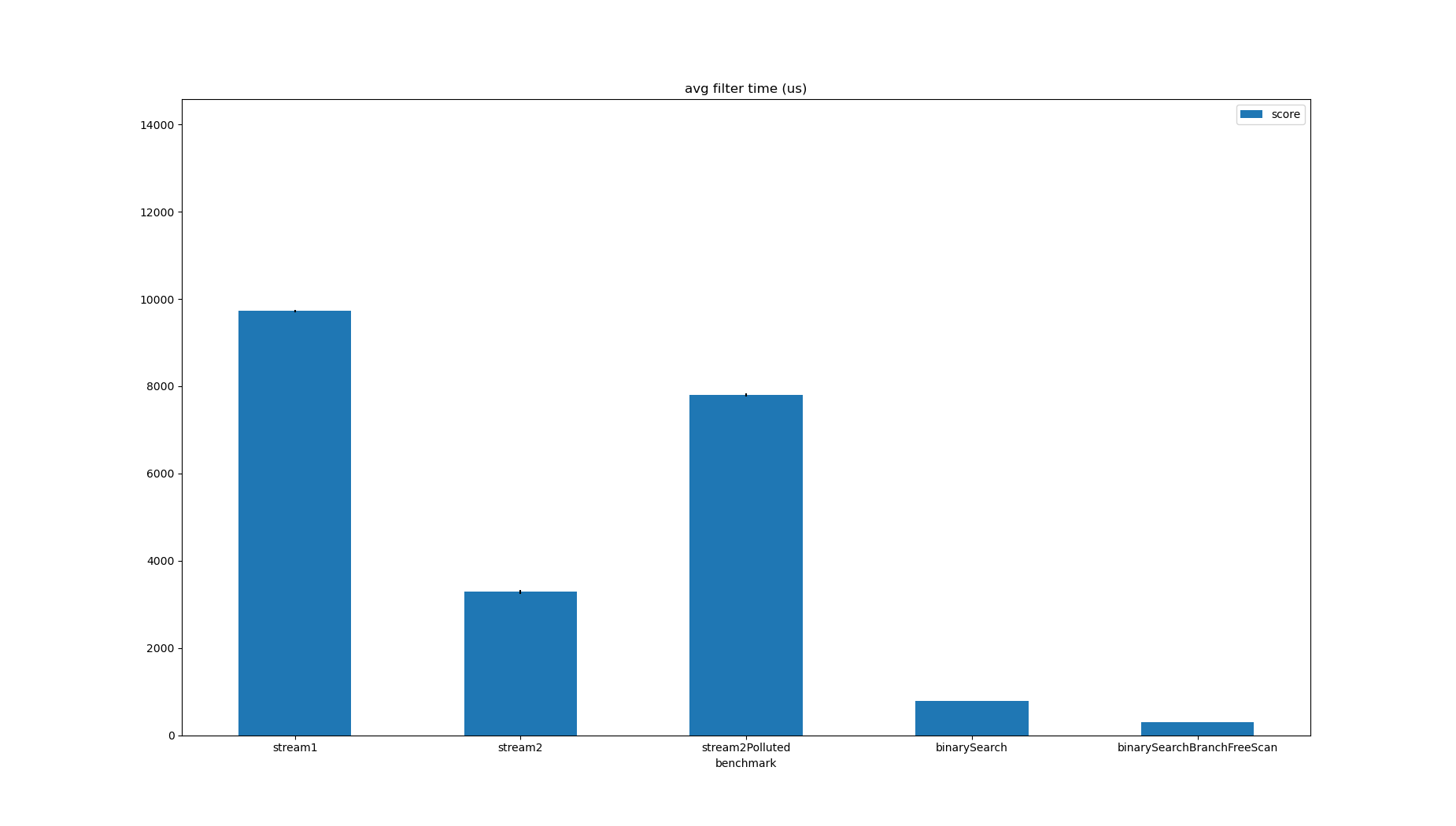
Inlining or no inlining, it’s inefficient to use linear search if the transactions are sorted, which they are (by time). As far as I’m aware there’s no way to communicate to the Stream API that a collection is already sorted and can be skipped over, and it doesn’t know how to crack filter predicates to exploit this anyway. So avoiding the Stream API and writing old fashioned Java code is effective. In the benchmark data, the time range predicate selects about 10% of the data, so the other two predicates should only apply to this much data. Assume the timestamps are unique for simplicity’s sake:
int first = Collections.binarySearch(transactions, new Transaction(0, 0, begin),
Comparator.comparingLong(Transaction::getTimestamp));
first = first < 0 ? -first - 1 : first;
int last = Collections.binarySearch(transactions, new Transaction(0, 0, end),
Comparator.comparingLong(Transaction::getTimestamp));
last = last < 0 ? -last - 1 : last;
long count = 0;
for (int i = first; i <= last; i++) {
Transaction transaction = transactions.get(i);
if (transaction.quantity >= qty && transaction.price <= price) {
count++;
}
}
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3283.291345 | 44.566458 | us/op | 100 | 1 | 1000000 |
| stream2Polluted | avgt | 1 | 5 | 7801.823477 | 41.229256 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 786.482285 | 1.994657 | us/op | 100 | 1 | 1000000 |
Sorting is not included in the benchmark time, but data is often naturally sorted by time.
It’s not a lot more code but goes a lot faster, and easier to measure because it’s so simple.
JMH’s perfnorm profiler shows that there is still a good number of branches missed, despite shedding about 90% of the work.
This means the instructions per cycle (IPC) is low:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| binarySearch | avgt | 1 | 5 | 786.482285 | 1.994657 | us/op | 100 | 1 | 1000000 |
| binarySearch:IPC | avgt | 1 | 1 | 0.755879 | NaN | insns/clk | 100 | 1 | 1000000 |
| binarySearch:branch-misses | avgt | 1 | 1 | 50739.339319 | NaN | #/op | 100 | 1 | 1000000 |
| binarySearch:branches | avgt | 1 | 1 | 434330.541115 | NaN | #/op | 100 | 1 | 1000000 |
This can be fixed by complicating the filter in the scan somewhat.
long count = 0;
for (int i = first; i <= last; i++) {
Transaction transaction = transactions.get(i);
count += (Math.min(1, Math.max(transaction.quantity - qty, 0))
+ Math.min(1, Math.max(price - transaction.price, 0))) >>> 1;
}
If the transaction’s quantity is greater than the threshold, Math.max(transaction.quantity - threshold, 0) will be positive, wrapping this in Math.min(1, x) means that the count will be one if the predicate holds and zero if it doesn’t.
This can be added to the other condition and divided by two so the count will be incremented by one when both conditions hold, and by zero when they don’t.
Math.max and Math.min are special and get compiled to conditional move instructions which aren’t speculated so can’t miss.
They are annotated as @IntrinsicCandidate:
@IntrinsicCandidate
public static int max(int a, int b) {
return (a >= b) ? a : b;
}
@IntrinsicCandidate
public static int min(int a, int b) {
return (a <= b) ? a : b;
}
This means if you have a hot loop, they should be preferred to inlining the equivalent logic, which may or may not be compiled to the same code. They’re also more readable, in my opinion. The branch misses basically disappear, and the instructions per cycle is now much higher:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| binarySearch | avgt | 1 | 5 | 786.482285 | 1.994657 | us/op | 100 | 1 | 1000000 |
| binarySearch:IPC | avgt | 1 | 1 | 0.755879 | NaN | insns/clk | 100 | 1 | 1000000 |
| binarySearch:branch-misses | avgt | 1 | 1 | 50739.339319 | NaN | #/op | 100 | 1 | 1000000 |
| binarySearch:branches | avgt | 1 | 1 | 434330.541115 | NaN | #/op | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan | avgt | 1 | 5 | 299.725900 | 2.414697 | us/op | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan:IPC | avgt | 1 | 1 | 3.278388 | NaN | insns/clk | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan:branch-misses | avgt | 1 | 1 | 524.965594 | NaN | #/op | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan:branches | avgt | 1 | 1 | 403042.075820 | NaN | #/op | 100 | 1 | 1000000 |
However, I am fairly certain that no analytical database written in Java implements counting over predicates like this. This is because fusing the predicate with aggregation is hostile to modularity, though generating code specialised to the problem is a good option if the implementation needs to be both fast and modular. It also won’t work with arbitrary numbers of predicates and needs to be padded to the next power of 2 so a matching result can be shifted down to one or zero in order to avoid integer division. If the JIT compiler were smarter and could inline the predicate evaluation into the count operator, I imagine it could transform modular code into this form, but it would probably get it wrong as often as it gets it right. So this is probably an artificially good result, but it is the best so far.
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3283.291345 | 44.566458 | us/op | 100 | 1 | 1000000 |
| stream2Polluted | avgt | 1 | 5 | 7801.823477 | 41.229256 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 786.482285 | 1.994657 | us/op | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan | avgt | 1 | 5 | 299.725900 | 2.414697 | us/op | 100 | 1 | 1000000 |
In my last post I used RangeBitmap - which is the data structure used in Apache Pinot’s range index - to select transactions matching the predicate.
Combined with binary search to apply the time range filter, it was much faster than any other implementation I measured.
I have recently implemented the ability to count values matching a predicate, instead of producing a bitmap of their offsets. The API is symmetric with the selection API:
long index(int qty, long price, long begin, long end) {
RoaringBitmap inTimeRange = timestampIndex.between(begin, end);
RoaringBitmap matchesQuantity = quantityIndex.gte(qty, inTimeRange);
return priceIndex.lteCardinality(price, matchesQuantity);
}
long binarySearchThenIndex(int qty, long price, long begin, long end) {
int first = Collections.binarySearch(transactions, new Transaction(0, 0, begin),
Comparator.comparingLong(Transaction::getTimestamp));
int last = Collections.binarySearch(transactions, new Transaction(0, 0, end),
Comparator.comparingLong(Transaction::getTimestamp));
RoaringBitmap inTimeRange = RoaringBitmap.bitmapOfRange(first, last + 1);
RoaringBitmap matchesQuantity = quantityIndex.gte(qty, inTimeRange);
return priceIndex.lteCardinality(price, matchesQuantity);
}
RangeBitmap is likely to be suboptimal for counting because the data structure is optimised for producing a sorted output set, which isn’t required for counting, but if you have a data stucture to support selection it ought to be able to provide a count without materialising intermediate results.
For selection, just using an index for all three attributes and combining the results was a lot faster than binarySearch but for counting it’s a little disappointing at the moment.
I haven’t tried to optimise the counting methods yet so there is probably a lot of low-hanging fruit.
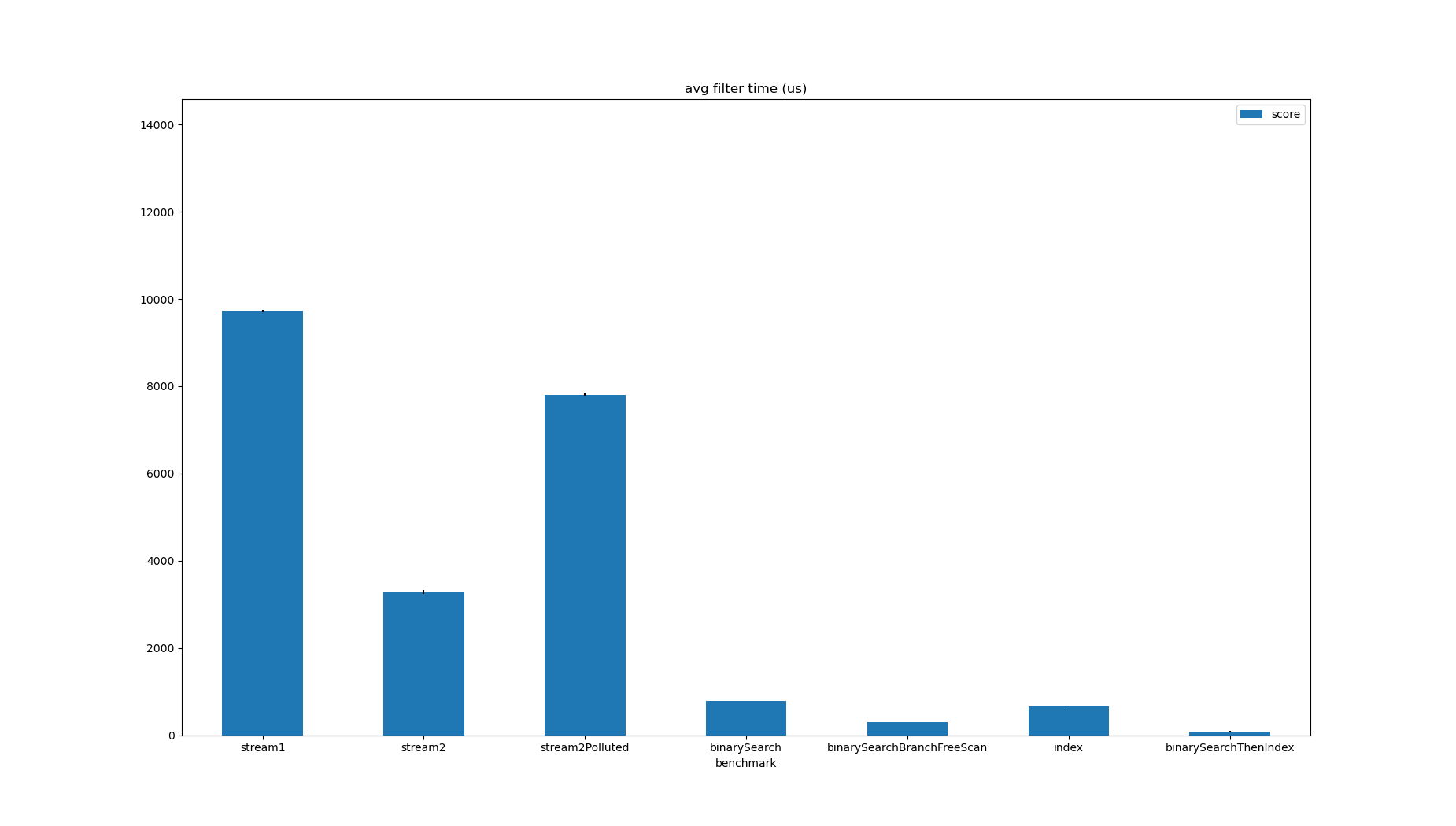
Cutting the range down with the binary search first produces a good result, even better than the hard to modularise binarySearchBranchFreeScan:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 9721.806835 | 27.935884 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3283.291345 | 44.566458 | us/op | 100 | 1 | 1000000 |
| stream2Polluted | avgt | 1 | 5 | 7801.823477 | 41.229256 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 786.482285 | 1.994657 | us/op | 100 | 1 | 1000000 |
| binarySearchBranchFreeScan | avgt | 1 | 5 | 299.725900 | 2.414697 | us/op | 100 | 1 | 1000000 |
| index | avgt | 1 | 5 | 666.951907 | 14.861610 | us/op | 100 | 1 | 1000000 |
| binarySearchThenIndex | avgt | 1 | 5 | 78.191544 | 17.903472 | us/op | 100 | 1 | 1000000 |
RangeBitmap was designed for use in Apache Pinot, so is compressed and supports zero-copy mapping to and from disk.
There are more details about how it works in depth in RangeBitmap - How range indexes work in Apache Pinot.
The benchmark used in this post is not particularly scientific but is here. If you want to run it, you will get different numbers, but the rank of each benchmark score should not change.