Evaluating Range Predicates
Suppose you are doing some kind of data analysis in Java, perhaps you are analysing transactions (as in sales made).
You have complex filters to evaluate before performing a calculation on Transaction objects.
public static final class Transaction {
private final int quantity;
private final long price;
private final long timestamp;
public Transaction(int quantity, long price, long timestamp) {
this.quantity = quantity;
this.price = price;
this.timestamp = timestamp;
}
public int getQuantity() {
return quantity;
}
public long getPrice() {
return price;
}
public long getTimestamp() {
return timestamp;
}
}
Suppose you want to find all transactions in a time range, and where the quantity exceeds a threshold but the price is lower than another threshold. This is clearly work that could be pushed down into a database, but you may not be able to do this for a couple of possible reasons:
- You don’t have huge data volumes but your management may have been convinced not to procure a proper database with a SQL interface
- You may not have a database because you have a lot of data, and it’s cheaper to store it in something like S3, you have processing jobs which filter the data programmatically
For whatever reason, you don’t have a database with a SQL interface and have to do the filtering yourself in a Java program, how might you do it?
You might use the streams API:
transactions.stream()
.filter(transaction -> transaction.quantity >= qty && transaction.price <= price
&& transaction.timestamp >= begin && transaction.timestamp <= end)
.forEach(this::processTransaction);
This will inspect every transaction to check if it matches the constraints. For 1M transactions, with parameters which select about 250 transactions, this takes about 10ms on my laptop:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
Suppose the transactions are actually sorted by time, the timestamp conditions should be predictable but aren’t evaluated first.
This means the unpredictable price and quantity conditions are evaluated for every transaction.
Reordering the conditions halves the runtime!
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3859.494033 | 42.012070 | us/op | 100 | 1 | 1000000 |
This is an interesting result, and JMH’s perfnorm profiler explains why:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
| stream1:branches | avgt | 1 | 5 | 4537456.732 | 100 | 1 | 1000000 | ||
| stream1:branch-misses | avgt | 1 | 5 | 505305.308 | 100 | 1 | 1000000 | ||
| stream1 | avgt | 1 | 5 | 3859.494033 | 42.012070 | us/op | 100 | 1 | 1000000 |
| stream2:branches | avgt | 1 | 5 | 4648262.253 | 100 | 1 | 1000000 | ||
| stream2:branch-misses | avgt | 1 | 5 | 51040.523 | 100 | 1 | 1000000 |
There are about the same number of branches in each case, but ~10x fewer branch misses. Branch misses are expensive!
However, if the transactions are sorted by time, linear search will be wasteful unless the timestamp range covers most of data.
In my benchmark, it covers about 10% of the data, so binary searching for the first and last timestamps in the range could correspond to up to ~10x improvement.
Assume the timestamps are unique for simplicity’s sake:
int first = Collections.binarySearch(state.transactions, new Transaction(0, 0, begin),
Comparator.comparingLong(Transaction::getTimestamp));
first = first < 0 ? -first - 1 : first;
int last = Collections.binarySearch(state.transactions, new Transaction(0, 0, end),
Comparator.comparingLong(Transaction::getTimestamp));
last = last < 0 ? -last - 1 : last;
for (int i = first; i <= last; i++) {
Transaction transaction = state.transactions.get(i);
if (transaction.quantity >= qty && transaction.price <= price) {
bh.consume(transaction);
}
}
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3859.494033 | 42.012070 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 1204.366198 | 8.455373 | us/op | 100 | 1 | 1000000 |
Sorting to ensure this is a valid application of binary search is not included in the benchmark time.
If several filters need to be evaluated against the collection, it would make sense to perform the sort to benefit from this.
This particular problem - applying range predicates to unsorted data - is solved by the RangeBitmap data structure in the RoaringBitmap library.
The data structure is immutable and benefits from knowledge of the range of values in the data set, but if several filters need to be evaluated, building an index on each attribute could be worth it.
The data structure has a build-then-use lifecycle:
long minTimestamp = Long.MAX_VALUE;
long maxTimestamp = Long.MIN_VALUE;
long minPrice = Long.MAX_VALUE;
long maxPrice = Long.MIN_VALUE;
int minQty = Long.MAX_VALUE;
int maxQty = Long.MIN_VALUE;
for (Transaction transaction : transactions) {
minTimestamp = Math.min(minTimestamp, transaction.getTimestamp());
maxTimestamp = Math.max(maxTimestamp, transaction.getTimestamp());
minPrice = Math.min(minPrice, transaction.getPrice());
maxPrice = Math.max(maxPrice, transaction.getPrice());
minQty = Math.min(minQty, transaction.getQuantity());
maxQty = Math.max(maxQty, transaction.getQuantity());
}
var timestampAppender = RangeBitmap.appender(maxTimestamp - minTimestamp);
var priceAppender = RangeBitmap.appender(maxPrice - minPrice);
var qtyAppender = RangeBitmap.appender(maxQty - minQty);
for (Transaction transaction : transactions) {
timestampAppender.add(transaction.getTimestamp() - minTimestamp);
priceAppender.add(transaction.getPrice() - minPrice);
qtyAppender.add(transaction.getQuantity() - minQty);
}
var timestampIndex = timestampAppender.build();
var priceIndex = priceAppender.build();
var qtyIndex = qtyAppender.build();
Whether the two passes over the data or the half page of code are worth it depends on how many filters you need to do and how fast they need to be.
RangeBitmap produces a RoaringBitmap of the indexes which satisfy a predicate, and can take RoaringBitmap parameters as inputs to skip over rows already filtered out.
The Streams API code used before is translated into RangeBitmap API calls:
RoaringBitmap inTimeRange = timestampIndex.between(minTimeThreshold - minTime, maxTimeThreshold - minTime);
RoaringBitmap matchesQuantity = qtyIndex.gte(minQtyThreshold - minQty, inTimeRange);
RoaringBitmap matchesPrice = priceIndex.lte(maxPriceThreshold - minPrice, matchesQuantity);
matchesPrice.forEach((IntConsumer) i -> processTransaction(transactions.get(i)));
}
The anchoring by the minimum values for each attribute is a little convoluted but improves efficiency (unless the minimum value is zero anyway) and this would be better abstracted by a convenience class in a real application. For the same data this is ~2x faster than the binary search approach:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3859.494033 | 42.012070 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 1204.366198 | 8.455373 | us/op | 100 | 1 | 1000000 |
| index | avgt | 1 | 5 | 690.562119 | 25.725005 | us/op | 100 | 1 | 1000000 |
Time spent building the index is not included in the benchmark time since it is assumed the filter will be applied several times and building the index will be amortised.
Binary search is much faster than the algorithm RangeBitmap uses, and it’s a shame it can only be used on one attribute since it’s not possible to do a global sort on more than one attribute.
If the data is sorted by timestamp, a hybrid approach can be taken:
int first = Collections.binarySearch(state.transactions, new Transaction(0, 0, begin),
Comparator.comparingLong(Transaction::getTimestamp));
first = first < 0 ? -first - 1 : first;
int last = Collections.binarySearch(state.transactions, new Transaction(0, 0, end),
Comparator.comparingLong(Transaction::getTimestamp));
last = last < 0 ? -last - 1 : last;
RoaringBitmap inTimeRange = RoaringBitmap.bitmapOfRange(first, last + 1);
RoaringBitmap matchesQuantity = qtyIndex.gte(maxPriceThreshold - minPrice, inTimeRange);
RoaringBitmap matchesPrice = priceIndex.lte(minQtyThreshold - minQty, matchesQuantity);
matchesPrice.forEach((IntConsumer) i -> processTransaction(state.transactions.get(i)));
This is over 100x faster than the original Streams API code and takes under 100us, all else being equal.
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: minPrice | Param: minQuantity | Param: size |
|---|---|---|---|---|---|---|---|---|---|
| stream1 | avgt | 1 | 5 | 8885.846120 | 41.192708 | us/op | 100 | 1 | 1000000 |
| stream2 | avgt | 1 | 5 | 3859.494033 | 42.012070 | us/op | 100 | 1 | 1000000 |
| binarySearch | avgt | 1 | 5 | 1204.366198 | 8.455373 | us/op | 100 | 1 | 1000000 |
| index | avgt | 1 | 5 | 690.562119 | 25.725005 | us/op | 100 | 1 | 1000000 |
| binarySearchThenIndex | avgt | 1 | 5 | 82.893010 | 12.486953 | us/op | 100 | 1 | 1000000 |
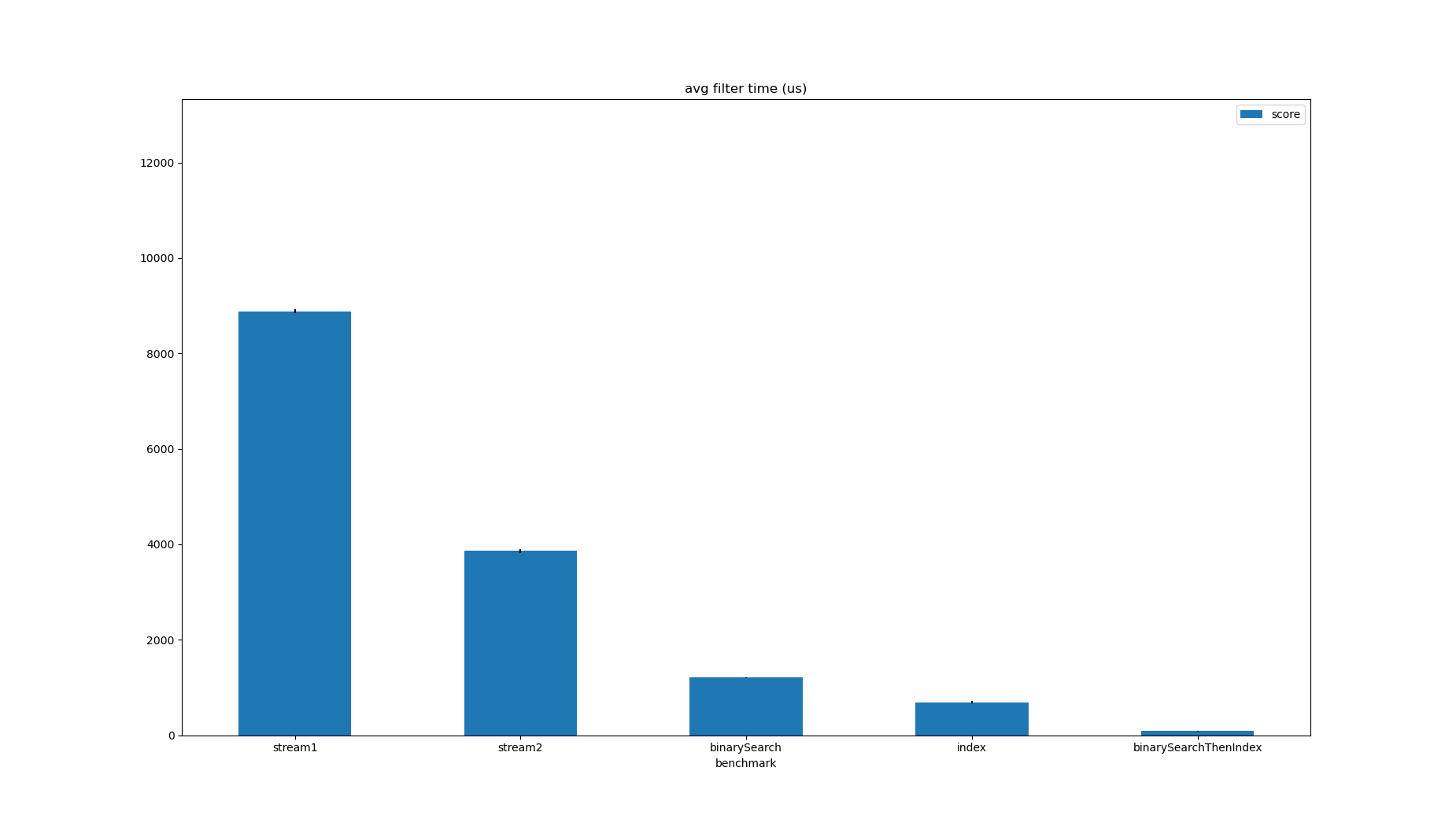
RangeBitmap was designed to power the range indexes in Apache Pinot, so is compressed and supports zero-copy mapping to and from disk.
There are more details about how it works in depth in RangeBitmap - How range indexes work in Apache Pinot.
It’s likely you’re sensible and pushing your filters down to your database to evaluate, but this data structure may be useful in some applications.
The benchmark used in this post is not particularly scientific but is here. If you want to run it, you will get different numbers, but the rank of each benchmark score should not change.