Building RoaringBitmaps from Streams
RoaringBitmap is a fast compressed bitset format. In the Java implementation of Roaring, it was until recently preferential to build a bitset in one go from sorted data; there were performance penalties of varying magnitude for incremental or unordered insertions. In a recent pull request, I wanted to improve incremental monotonic insertion so I could build bitmaps from streams, but sped up unsorted batch creation significantly by accident.
Incremental Ordered Insertion
If you want to build a bitmap, you can do so efficiently with the RoaringBitmap.bitmapOf factory method.
int[] data = ...
RoaringBitmap bitmap = RoaringBitmap.bitmapOf(data);
However, I often find that I want to stream integers into a bitmap. Given that the integers being inserted into a bitmap often represent indices into an array, such a stream is likely to be monotonic. You might implement this like so:
IntStream stream = ...
RoaringBitmap bitmap = new RoaringBitmap();
stream.forEach(bitmap::add);
While this is OK, it has a few inefficiencies compared to the batch creation method.
- Indirection: the container being written to must be located on each insertion
- Eagerness: the cardinality must be kept up to date on each insertion
- Allocation pressure: the best container type can't be known in advance. Choice of container may change as data is inserted, this requires allocations of new instances.
You could also collect the stream into an int[] and use the batch method, but it could be a large temporary object with obvious drawbacks.
OrderedWriter
The solution I proposed is to create a writer object (OrderedWriter) which allocates a small buffer of 8KB, to use as a bitmap large enough to cover 16 bits. The stream to bitmap code becomes:
IntStream stream = ...
RoaringBitmap bitmap = new RoaringBitmap();
OrderedWriter writer = new OrderedWriter(bitmap);
stream.forEach(writer::add);
writer.flush(); // clear the buffer out
This is implemented so that changes in key (where the most significant 16 bits of each integer is stored) trigger a flush of the buffer.
public void add(int value) {
short key = Util.highbits(value);
short low = Util.lowbits(value);
if (key != currentKey) {
if (Util.compareUnsigned(key, currentKey) < 0) {
throw new IllegalStateException("Must write in ascending key order");
}
flush();
}
int ulow = low & 0xFFFF;
bitmap[(ulow >>> 6)] |= (1L << ulow);
currentKey = key;
dirty = true;
}
When a flush occurs, a container type is chosen and appended to the bitmap’s prefix index.
public void flush() {
if (dirty) {
RoaringArray highLowContainer = underlying.highLowContainer;
// we check that it's safe to append since RoaringArray.append does no validation
if (highLowContainer.size > 0) {
short key = highLowContainer.getKeyAtIndex(highLowContainer.size - 1);
if (Util.compareUnsigned(currentKey, key) <= 0) {
throw new IllegalStateException("Cannot write " + currentKey + " after " + key);
}
}
highLowContainer.append(currentKey, chooseBestContainer());
clearBitmap();
dirty = false;
}
}
There are significant performance advantages in this approach. There is no indirection cost, and no searches in the prefix index for containers: the writes are just buffered. The buffer is small enough to fit in cache, and containers only need to be created when the writer is flushed, which happens whenever a new key is seen, or when flush is called manually. During a flush, the cardinality can be computed in one go, the best container can be chosen, and run optimisation only has to happen once. Computing the cardinality is the only bottleneck - it requires 1024 calls to Long.bitCount which can’t be vectorised in a language like Java. It can’t be incremented on insertion without either sacrificing idempotence or incurring the cost of a membership check. After the flush, the buffer needs to be cleared, using a call to Arrays.fill which is vectorised. So, despite the cost of the buffer, this can be quite efficient.
This approach isn’t universally applicable. For instance, you must write data in ascending order of the most significant 16 bits. You must also remember to flush the writer when you’re finished: until you’ve called flush, the data in the last container may not be in the bitmap. For my particular use case, this is reasonable. However, there are times when this is not fit for purpose, such as if you are occasionally inserting values and expect them to be available to queries immediately. In general, if you don’t know when you’ll stop adding data to the bitmap, this isn’t a good fit because you won’t know when to call flush.
Benchmark
I benchmarked the two approaches, varying bitmap sizes and randomness (likelihood of there not being a compressible run), and was amazed to find that this approach actually beats having a sorted array and using RoaringBitmap.bitmapOf. Less surprising was beating the existing API for incremental adds (this was the goal in the first place). Lower is better:
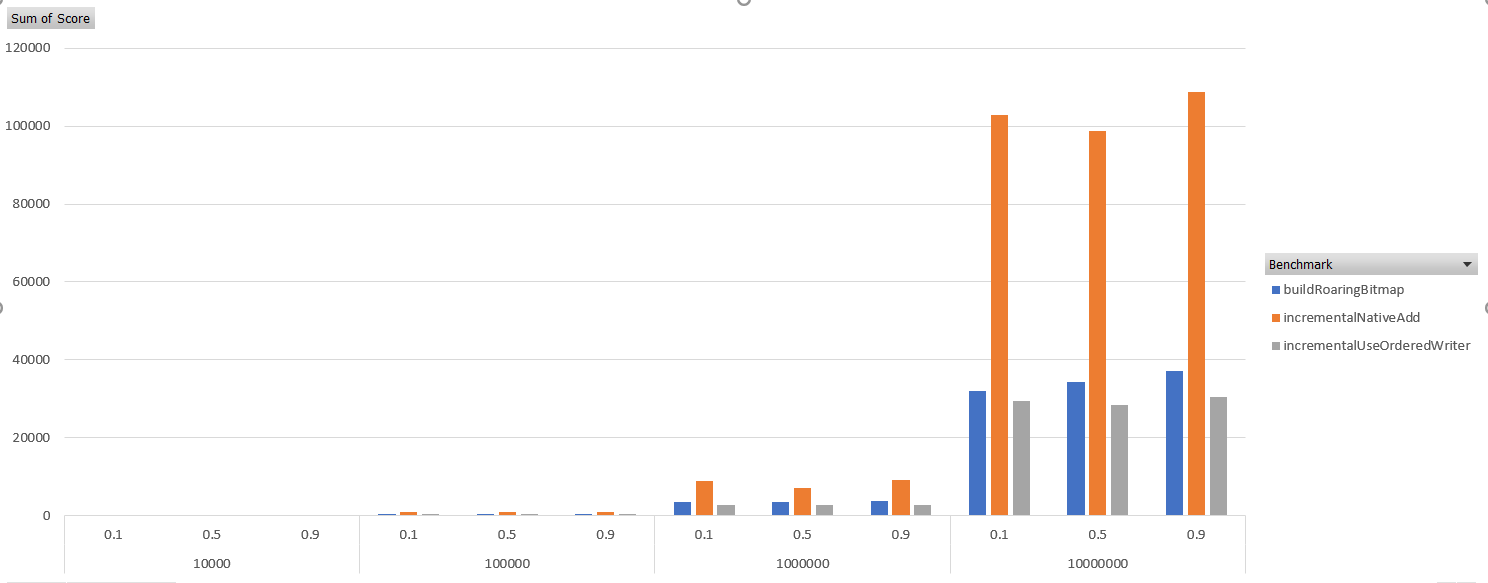
| Benchmark | (randomness) | (size) | Mode | Cnt | Score | Error | Units |
|---|---|---|---|---|---|---|---|
| buildRoaringBitmap | 0.1 | 10000 | avgt | 5 | 54.263 | 3.393 | us/op |
| buildRoaringBitmap | 0.1 | 100000 | avgt | 5 | 355.188 | 15.234 | us/op |
| buildRoaringBitmap | 0.1 | 1000000 | avgt | 5 | 3567.839 | 135.149 | us/op |
| buildRoaringBitmap | 0.1 | 10000000 | avgt | 5 | 31982.046 | 1227.325 | us/op |
| buildRoaringBitmap | 0.5 | 10000 | avgt | 5 | 53.855 | 0.887 | us/op |
| buildRoaringBitmap | 0.5 | 100000 | avgt | 5 | 357.671 | 14.111 | us/op |
| buildRoaringBitmap | 0.5 | 1000000 | avgt | 5 | 3556.152 | 243.671 | us/op |
| buildRoaringBitmap | 0.5 | 10000000 | avgt | 5 | 34385.971 | 3864.143 | us/op |
| buildRoaringBitmap | 0.9 | 10000 | avgt | 5 | 59.354 | 10.385 | us/op |
| buildRoaringBitmap | 0.9 | 100000 | avgt | 5 | 374.245 | 54.485 | us/op |
| buildRoaringBitmap | 0.9 | 1000000 | avgt | 5 | 3712.684 | 657.964 | us/op |
| buildRoaringBitmap | 0.9 | 10000000 | avgt | 5 | 37223.976 | 4691.297 | us/op |
| incrementalNativeAdd | 0.1 | 10000 | avgt | 5 | 115.213 | 31.909 | us/op |
| incrementalNativeAdd | 0.1 | 100000 | avgt | 5 | 911.925 | 127.922 | us/op |
| incrementalNativeAdd | 0.1 | 1000000 | avgt | 5 | 8889.49 | 320.821 | us/op |
| incrementalNativeAdd | 0.1 | 10000000 | avgt | 5 | 102819.877 | 14247.868 | us/op |
| incrementalNativeAdd | 0.5 | 10000 | avgt | 5 | 116.878 | 28.232 | us/op |
| incrementalNativeAdd | 0.5 | 100000 | avgt | 5 | 947.076 | 128.255 | us/op |
| incrementalNativeAdd | 0.5 | 1000000 | avgt | 5 | 7190.443 | 202.012 | us/op |
| incrementalNativeAdd | 0.5 | 10000000 | avgt | 5 | 98843.303 | 4325.924 | us/op |
| incrementalNativeAdd | 0.9 | 10000 | avgt | 5 | 101.694 | 6.579 | us/op |
| incrementalNativeAdd | 0.9 | 100000 | avgt | 5 | 816.411 | 65.678 | us/op |
| incrementalNativeAdd | 0.9 | 1000000 | avgt | 5 | 9114.624 | 412.152 | us/op |
| incrementalNativeAdd | 0.9 | 10000000 | avgt | 5 | 108793.694 | 22562.527 | us/op |
| incrementalUseOrderedWriter | 0.1 | 10000 | avgt | 5 | 23.573 | 5.962 | us/op |
| incrementalUseOrderedWriter | 0.1 | 100000 | avgt | 5 | 289.588 | 36.814 | us/op |
| incrementalUseOrderedWriter | 0.1 | 1000000 | avgt | 5 | 2785.659 | 49.385 | us/op |
| incrementalUseOrderedWriter | 0.1 | 10000000 | avgt | 5 | 29489.758 | 2601.39 | us/op |
| incrementalUseOrderedWriter | 0.5 | 10000 | avgt | 5 | 23.57 | 1.536 | us/op |
| incrementalUseOrderedWriter | 0.5 | 100000 | avgt | 5 | 276.488 | 9.662 | us/op |
| incrementalUseOrderedWriter | 0.5 | 1000000 | avgt | 5 | 2799.408 | 198.77 | us/op |
| incrementalUseOrderedWriter | 0.5 | 10000000 | avgt | 5 | 28313.626 | 1976.042 | us/op |
| incrementalUseOrderedWriter | 0.9 | 10000 | avgt | 5 | 22.345 | 1.574 | us/op |
| incrementalUseOrderedWriter | 0.9 | 100000 | avgt | 5 | 280.205 | 36.987 | us/op |
| incrementalUseOrderedWriter | 0.9 | 1000000 | avgt | 5 | 2779.732 | 93.456 | us/op |
| incrementalUseOrderedWriter | 0.9 | 10000000 | avgt | 5 | 30568.591 | 2140.826 | us/op |
These benchmarks don’t go far enough to support replacing RoaringBitmap.bitmapOf.
Unsorted Input Data
In the cases benchmarked, this approach seems to be worthwhile. I can’t actually think of a case where someone would want to build a bitmap from unsorted data, but it occurred to me that this approach might be fast enough to cover the cost of a sort. OrderedWriter is also relaxed enough that it only needs the most significant 16 bits to be monotonic, so a full sort isn’t necessary. Implementing a radix sort on the most significant 16 bits (stable in the least significant 16 bits), prior to incremental insertion via an OrderedWriter, leads to huge increases in performance over RoaringBitmap.bitmapOf. The implementation is as follows:
public static RoaringBitmap bitmapOfUnordered(final int... data) {
partialRadixSort(data);
RoaringBitmap bitmap = new RoaringBitmap();
OrderedWriter writer = new OrderedWriter(bitmap);
for (int i : data) {
writer.add(i);
}
writer.flush();
return bitmap;
}
It did very well, according to benchmarks, even against various implementations of sort prior to RoaringBitmap.bitmapOf. Lower is better:
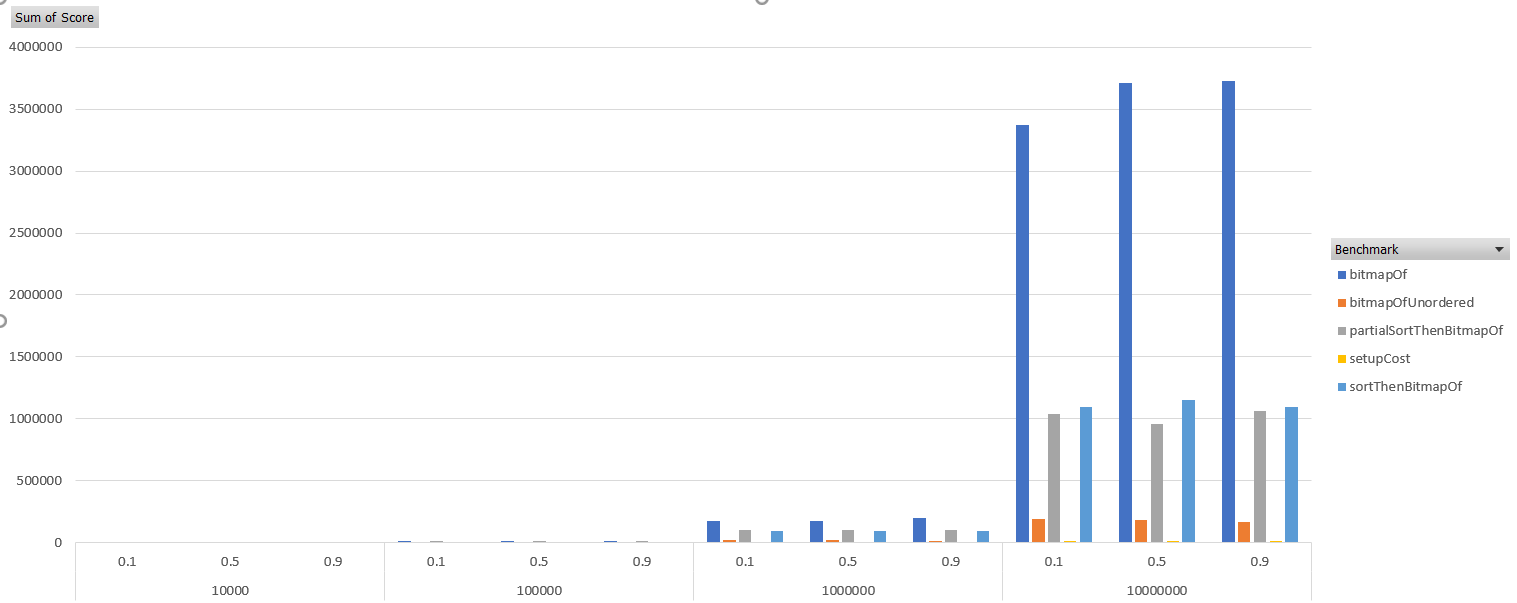
| Benchmark | (randomness) | (size) | Mode | Cnt | Score | Error | Units |
|---|---|---|---|---|---|---|---|
| bitmapOf | 0.1 | 10000 | avgt | 5 | 1058.106 | 76.013 | us/op |
| bitmapOf | 0.1 | 100000 | avgt | 5 | 12323.905 | 976.68 | us/op |
| bitmapOf | 0.1 | 1000000 | avgt | 5 | 171812.526 | 9593.879 | us/op |
| bitmapOf | 0.1 | 10000000 | avgt | 5 | 3376296.157 | 170362.195 | us/op |
| bitmapOf | 0.5 | 10000 | avgt | 5 | 1096.663 | 477.795 | us/op |
| bitmapOf | 0.5 | 100000 | avgt | 5 | 12836.177 | 1674.54 | us/op |
| bitmapOf | 0.5 | 1000000 | avgt | 5 | 171998.126 | 4176 | us/op |
| bitmapOf | 0.5 | 10000000 | avgt | 5 | 3707804.439 | 974532.361 | us/op |
| bitmapOf | 0.9 | 10000 | avgt | 5 | 1124.881 | 65.673 | us/op |
| bitmapOf | 0.9 | 100000 | avgt | 5 | 14585.589 | 1894.788 | us/op |
| bitmapOf | 0.9 | 1000000 | avgt | 5 | 198506.813 | 8552.218 | us/op |
| bitmapOf | 0.9 | 10000000 | avgt | 5 | 3723942.934 | 423704.363 | us/op |
| bitmapOfUnordered | 0.1 | 10000 | avgt | 5 | 174.583 | 17.475 | us/op |
| bitmapOfUnordered | 0.1 | 100000 | avgt | 5 | 1768.613 | 86.543 | us/op |
| bitmapOfUnordered | 0.1 | 1000000 | avgt | 5 | 17889.705 | 135.714 | us/op |
| bitmapOfUnordered | 0.1 | 10000000 | avgt | 5 | 192645.352 | 6482.726 | us/op |
| bitmapOfUnordered | 0.5 | 10000 | avgt | 5 | 157.351 | 3.254 | us/op |
| bitmapOfUnordered | 0.5 | 100000 | avgt | 5 | 1674.919 | 90.138 | us/op |
| bitmapOfUnordered | 0.5 | 1000000 | avgt | 5 | 16900.458 | 778.999 | us/op |
| bitmapOfUnordered | 0.5 | 10000000 | avgt | 5 | 185399.32 | 4383.485 | us/op |
| bitmapOfUnordered | 0.9 | 10000 | avgt | 5 | 145.642 | 1.257 | us/op |
| bitmapOfUnordered | 0.9 | 100000 | avgt | 5 | 1515.845 | 82.914 | us/op |
| bitmapOfUnordered | 0.9 | 1000000 | avgt | 5 | 15807.597 | 811.048 | us/op |
| bitmapOfUnordered | 0.9 | 10000000 | avgt | 5 | 167863.49 | 3501.132 | us/op |
| partialSortThenBitmapOf | 0.1 | 10000 | avgt | 5 | 1060.152 | 168.802 | us/op |
| partialSortThenBitmapOf | 0.1 | 100000 | avgt | 5 | 10942.731 | 347.583 | us/op |
| partialSortThenBitmapOf | 0.1 | 1000000 | avgt | 5 | 100606.506 | 24705.341 | us/op |
| partialSortThenBitmapOf | 0.1 | 10000000 | avgt | 5 | 1035448.545 | 157383.713 | us/op |
| partialSortThenBitmapOf | 0.5 | 10000 | avgt | 5 | 1029.883 | 100.291 | us/op |
| partialSortThenBitmapOf | 0.5 | 100000 | avgt | 5 | 10472.509 | 832.719 | us/op |
| partialSortThenBitmapOf | 0.5 | 1000000 | avgt | 5 | 101144.032 | 16908.087 | us/op |
| partialSortThenBitmapOf | 0.5 | 10000000 | avgt | 5 | 958242.087 | 39650.946 | us/op |
| partialSortThenBitmapOf | 0.9 | 10000 | avgt | 5 | 1008.413 | 70.999 | us/op |
| partialSortThenBitmapOf | 0.9 | 100000 | avgt | 5 | 10458.34 | 600.416 | us/op |
| partialSortThenBitmapOf | 0.9 | 1000000 | avgt | 5 | 103945.644 | 2026.26 | us/op |
| partialSortThenBitmapOf | 0.9 | 10000000 | avgt | 5 | 1065638.269 | 102257.059 | us/op |
| setupCost | 0.1 | 10000 | avgt | 5 | 6.577 | 0.121 | us/op |
| setupCost | 0.1 | 100000 | avgt | 5 | 61.378 | 24.113 | us/op |
| setupCost | 0.1 | 1000000 | avgt | 5 | 1021.588 | 536.68 | us/op |
| setupCost | 0.1 | 10000000 | avgt | 5 | 13182.341 | 196.773 | us/op |
| setupCost | 0.5 | 10000 | avgt | 5 | 7.139 | 2.216 | us/op |
| setupCost | 0.5 | 100000 | avgt | 5 | 60.847 | 23.395 | us/op |
| setupCost | 0.5 | 1000000 | avgt | 5 | 800.888 | 14.711 | us/op |
| setupCost | 0.5 | 10000000 | avgt | 5 | 13431.625 | 553.44 | us/op |
| setupCost | 0.9 | 10000 | avgt | 5 | 6.599 | 0.09 | us/op |
| setupCost | 0.9 | 100000 | avgt | 5 | 60.946 | 22.511 | us/op |
| setupCost | 0.9 | 1000000 | avgt | 5 | 813.445 | 4.896 | us/op |
| setupCost | 0.9 | 10000000 | avgt | 5 | 13374.943 | 349.314 | us/op |
| sortThenBitmapOf | 0.1 | 10000 | avgt | 5 | 636.23 | 13.423 | us/op |
| sortThenBitmapOf | 0.1 | 100000 | avgt | 5 | 7411.756 | 174.264 | us/op |
| sortThenBitmapOf | 0.1 | 1000000 | avgt | 5 | 92299.305 | 3651.161 | us/op |
| sortThenBitmapOf | 0.1 | 10000000 | avgt | 5 | 1096374.443 | 162575.234 | us/op |
| sortThenBitmapOf | 0.5 | 10000 | avgt | 5 | 634.957 | 47.447 | us/op |
| sortThenBitmapOf | 0.5 | 100000 | avgt | 5 | 7939.074 | 409.328 | us/op |
| sortThenBitmapOf | 0.5 | 1000000 | avgt | 5 | 93505.427 | 5409.749 | us/op |
| sortThenBitmapOf | 0.5 | 10000000 | avgt | 5 | 1147933.592 | 57485.51 | us/op |
| sortThenBitmapOf | 0.9 | 10000 | avgt | 5 | 661.072 | 6.717 | us/op |
| sortThenBitmapOf | 0.9 | 100000 | avgt | 5 | 7915.506 | 356.148 | us/op |
| sortThenBitmapOf | 0.9 | 1000000 | avgt | 5 | 93403.343 | 5454.583 | us/op |
| sortThenBitmapOf | 0.9 | 10000000 | avgt | 5 | 1095960.734 | 85753.917 | us/op |
It looks like there are good performance gains available here, but these things tend to depend on particular data sets. I would be interested in hearing from anyone who has tried to use this class in a real application.