Multiplying Matrices, Fast and Slow
I recently read a very interesting blog post about exposing Intel SIMD intrinsics via a fork of the Scala compiler (scala-virtualized), which reports multiplicative improvements in throughput over HotSpot JIT compiled code. The academic paper (SIMD Intrinsics on Managed Language Runtimes), which has been accepted at CGO 2018, proposes a powerful alternative to the traditional JVM approach of pairing dumb programmers with a (hopefully) smart JIT compiler. Lightweight Modular Staging (LMS) allows the generation of an executable binary from a high level representation: handcrafted representations of vectorised algorithms, written in a dialect of Scala, can be compiled natively and later invoked with a single JNI call. This approach bypasses C2 without incurring excessive JNI costs. The freely available benchmarks can be easily run to reproduce the results in the paper, which is an achievement in itself, but some of the Java implementations used as baselines look less efficient than they could be. This post is about improving the efficiency of the Java matrix multiplication the LMS generated code is benchmarked against. Despite finding edge cases where autovectorisation fails, I find it is possible to get performance comparable to LMS with plain Java (and a JDK upgrade).
Two implementations of Java matrix multiplication are provided in the NGen benchmarks: JMMM.baseline - a naive but cache unfriendly matrix multiplication - and JMMM.blocked which is supplied as an improvement. JMMM.blocked is something of a local maximum because it does manual loop unrolling: this actually removes the trigger for autovectorisation analysis. I provide a simple and cache-efficient Java implementation (with the same asymptotic complexity, the improvement is just technical) and benchmark these implementations using JDK8 and the soon to be released JDK10 separately.
public void fast(float[] a, float[] b, float[] c, int n) {
int in = 0;
for (int i = 0; i < n; ++i) {
int kn = 0;
for (int k = 0; k < n; ++k) {
float aik = a[in + k];
for (int j = 0; j < n; ++j) {
c[in + j] += aik * b[kn + j];
}
kn += n;
}
in += n;
}
}
With JDK 1.8.0_131, the “fast” implementation is only 2x faster than the blocked algorithm; this is nowhere near fast enough to match LMS. In fact, LMS does a lot better than 5x blocked (6x-8x) on my Skylake laptop at 2.6GHz, and performs between 2x and 4x better than the improved implementation. Flops / Cycle is calculated as size ^ 3 * 2 / CPU frequency Hz.
====================================================
Benchmarking MMM.jMMM.fast (JVM implementation)
----------------------------------------------------
Size (N) | Flops / Cycle
----------------------------------------------------
8 | 0.4994459272
32 | 1.0666533335
64 | 0.9429120397
128 | 0.9692385519
192 | 0.9796619688
256 | 1.0141446247
320 | 0.9894415771
384 | 1.0046245750
448 | 1.0221353392
512 | 0.9943527764
576 | 0.9952093603
640 | 0.9854689714
704 | 0.9947153752
768 | 1.0197765248
832 | 1.0479691069
896 | 1.0060121097
960 | 0.9937347412
1024 | 0.9056494897
====================================================
====================================================
Benchmarking MMM.nMMM.blocked (LMS generated)
----------------------------------------------------
Size (N) | Flops / Cycle
----------------------------------------------------
8 | 0.2500390686
32 | 3.9999921875
64 | 4.1626523901
128 | 4.4618695374
192 | 3.9598982956
256 | 4.3737341517
320 | 4.2412225389
384 | 3.9640163416
448 | 4.0957167537
512 | 3.3801071278
576 | 4.1869326167
640 | 3.8225244883
704 | 3.8648224140
768 | 3.5240611589
832 | 3.7941562681
896 | 3.1735179981
960 | 2.5856903789
1024 | 1.7817152313
====================================================
====================================================
Benchmarking MMM.jMMM.blocked (JVM implementation)
----------------------------------------------------
Size (N) | Flops / Cycle
----------------------------------------------------
8 | 0.3333854248
32 | 0.6336670915
64 | 0.5733484649
128 | 0.5987433798
192 | 0.5819900921
256 | 0.5473562109
320 | 0.5623263520
384 | 0.5583823292
448 | 0.5657882256
512 | 0.5430879470
576 | 0.5269635678
640 | 0.5595204791
704 | 0.5297557807
768 | 0.5493631388
832 | 0.5471832673
896 | 0.4769554752
960 | 0.4985080443
1024 | 0.4014589400
====================================================
JDK10 is about to be released so it’s worth looking at the effect of recent improvements to C2, including better use of AVX2 and support for vectorised FMA. Since LMS depends on scala-virtualized, which currently only supports Scala 2.11, the LMS implementation cannot be run with a more recent JDK so its performance running in JDK10 could only be extrapolated. Since its raison d’être is to bypass C2, it could be reasonably assumed it is insulated from JVM performance improvements (or regressions). Measurements of floating point operations per cycle provide a sensible comparison, in any case.
Moving away from ScalaMeter, I created a JMH benchmark to see how matrix multiplication behaves in JDK10.
@OutputTimeUnit(TimeUnit.SECONDS)
@State(Scope.Benchmark)
public class MMM {
@Param({"8", "32", "64", "128", "192", "256", "320", "384", "448", "512" , "576", "640", "704", "768", "832", "896", "960", "1024"})
int size;
private float[] a;
private float[] b;
private float[] c;
@Setup(Level.Trial)
public void init() {
a = DataUtil.createFloatArray(size * size);
b = DataUtil.createFloatArray(size * size);
c = new float[size * size];
}
@Benchmark
public void fast(Blackhole bh) {
fast(a, b, c, size);
bh.consume(c);
}
@Benchmark
public void baseline(Blackhole bh) {
baseline(a, b, c, size);
bh.consume(c);
}
@Benchmark
public void blocked(Blackhole bh) {
blocked(a, b, c, size);
bh.consume(c);
}
//
// Baseline implementation of a Matrix-Matrix-Multiplication
//
public void baseline (float[] a, float[] b, float[] c, int n){
for (int i = 0; i < n; i += 1) {
for (int j = 0; j < n; j += 1) {
float sum = 0.0f;
for (int k = 0; k < n; k += 1) {
sum += a[i * n + k] * b[k * n + j];
}
c[i * n + j] = sum;
}
}
}
//
// Blocked version of MMM, reference implementation available at:
// http://csapp.cs.cmu.edu/2e/waside/waside-blocking.pdf
//
public void blocked(float[] a, float[] b, float[] c, int n) {
int BLOCK_SIZE = 8;
for (int kk = 0; kk < n; kk += BLOCK_SIZE) {
for (int jj = 0; jj < n; jj += BLOCK_SIZE) {
for (int i = 0; i < n; i++) {
for (int j = jj; j < jj + BLOCK_SIZE; ++j) {
float sum = c[i * n + j];
for (int k = kk; k < kk + BLOCK_SIZE; ++k) {
sum += a[i * n + k] * b[k * n + j];
}
c[i * n + j] = sum;
}
}
}
}
}
public void fast(float[] a, float[] b, float[] c, int n) {
int in = 0;
for (int i = 0; i < n; ++i) {
int kn = 0;
for (int k = 0; k < n; ++k) {
float aik = a[in + k];
for (int j = 0; j < n; ++j) {
c[in + j] = Math.fma(aik, b[kn + j], c[in + j]);
}
kn += n;
}
in += n;
}
}
}
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: size | Ratio to blocked | Flops/Cycle |
|---|---|---|---|---|---|---|---|---|---|
| baseline | thrpt | 1 | 10 | 1228544.82 | 38793.17392 | ops/s | 8 | 1.061598336 | 0.483857652 |
| baseline | thrpt | 1 | 10 | 22973.03402 | 1012.043446 | ops/s | 32 | 1.302266947 | 0.57906183 |
| baseline | thrpt | 1 | 10 | 2943.088879 | 221.57475 | ops/s | 64 | 1.301414733 | 0.593471609 |
| baseline | thrpt | 1 | 10 | 358.010135 | 9.342801 | ops/s | 128 | 1.292889618 | 0.577539747 |
| baseline | thrpt | 1 | 10 | 105.758366 | 4.275503 | ops/s | 192 | 1.246415143 | 0.575804515 |
| baseline | thrpt | 1 | 10 | 41.465557 | 1.112753 | ops/s | 256 | 1.430003946 | 0.535135851 |
| baseline | thrpt | 1 | 10 | 20.479081 | 0.462547 | ops/s | 320 | 1.154267894 | 0.516198866 |
| baseline | thrpt | 1 | 10 | 11.686685 | 0.263476 | ops/s | 384 | 1.186535349 | 0.509027985 |
| baseline | thrpt | 1 | 10 | 7.344184 | 0.269656 | ops/s | 448 | 1.166421127 | 0.507965526 |
| baseline | thrpt | 1 | 10 | 3.545153 | 0.108086 | ops/s | 512 | 0.81796657 | 0.366017216 |
| baseline | thrpt | 1 | 10 | 3.789384 | 0.130934 | ops/s | 576 | 1.327168294 | 0.557048123 |
| baseline | thrpt | 1 | 10 | 1.981957 | 0.040136 | ops/s | 640 | 1.020965271 | 0.399660104 |
| baseline | thrpt | 1 | 10 | 1.76672 | 0.036386 | ops/s | 704 | 1.168272442 | 0.474179037 |
| baseline | thrpt | 1 | 10 | 1.01026 | 0.049853 | ops/s | 768 | 0.845514112 | 0.352024966 |
| baseline | thrpt | 1 | 10 | 1.115814 | 0.03803 | ops/s | 832 | 1.148752171 | 0.494331667 |
| baseline | thrpt | 1 | 10 | 0.703561 | 0.110626 | ops/s | 896 | 0.938435436 | 0.389298235 |
| baseline | thrpt | 1 | 10 | 0.629896 | 0.052448 | ops/s | 960 | 1.081741651 | 0.428685898 |
| baseline | thrpt | 1 | 10 | 0.407772 | 0.019079 | ops/s | 1024 | 1.025356561 | 0.336801424 |
| blocked | thrpt | 1 | 10 | 1157259.558 | 49097.48711 | ops/s | 8 | 1 | 0.455782226 |
| blocked | thrpt | 1 | 10 | 17640.8025 | 1226.401298 | ops/s | 32 | 1 | 0.444656782 |
| blocked | thrpt | 1 | 10 | 2261.453481 | 98.937035 | ops/s | 64 | 1 | 0.456020355 |
| blocked | thrpt | 1 | 10 | 276.906961 | 22.851857 | ops/s | 128 | 1 | 0.446704605 |
| blocked | thrpt | 1 | 10 | 84.850033 | 4.441454 | ops/s | 192 | 1 | 0.461968485 |
| blocked | thrpt | 1 | 10 | 28.996813 | 7.585551 | ops/s | 256 | 1 | 0.374219842 |
| blocked | thrpt | 1 | 10 | 17.742052 | 0.627629 | ops/s | 320 | 1 | 0.447208892 |
| blocked | thrpt | 1 | 10 | 9.84942 | 0.367603 | ops/s | 384 | 1 | 0.429003641 |
| blocked | thrpt | 1 | 10 | 6.29634 | 0.402846 | ops/s | 448 | 1 | 0.435490676 |
| blocked | thrpt | 1 | 10 | 4.334105 | 0.384849 | ops/s | 512 | 1 | 0.447472097 |
| blocked | thrpt | 1 | 10 | 2.85524 | 0.199102 | ops/s | 576 | 1 | 0.419726816 |
| blocked | thrpt | 1 | 10 | 1.941258 | 0.10915 | ops/s | 640 | 1 | 0.391453182 |
| blocked | thrpt | 1 | 10 | 1.51225 | 0.076621 | ops/s | 704 | 1 | 0.40588053 |
| blocked | thrpt | 1 | 10 | 1.194847 | 0.063147 | ops/s | 768 | 1 | 0.416344283 |
| blocked | thrpt | 1 | 10 | 0.971327 | 0.040421 | ops/s | 832 | 1 | 0.430320551 |
| blocked | thrpt | 1 | 10 | 0.749717 | 0.042997 | ops/s | 896 | 1 | 0.414837526 |
| blocked | thrpt | 1 | 10 | 0.582298 | 0.016725 | ops/s | 960 | 1 | 0.39629231 |
| blocked | thrpt | 1 | 10 | 0.397688 | 0.043639 | ops/s | 1024 | 1 | 0.328472491 |
| fast | thrpt | 1 | 10 | 1869676.345 | 76416.50848 | ops/s | 8 | 1.615606743 | 0.736364837 |
| fast | thrpt | 1 | 10 | 48485.47216 | 1301.926828 | ops/s | 32 | 2.748484496 | 1.222132271 |
| fast | thrpt | 1 | 10 | 6431.341657 | 153.905413 | ops/s | 64 | 2.843897392 | 1.296875098 |
| fast | thrpt | 1 | 10 | 840.601821 | 45.998723 | ops/s | 128 | 3.035683242 | 1.356053685 |
| fast | thrpt | 1 | 10 | 260.386996 | 13.022418 | ops/s | 192 | 3.068790745 | 1.417684611 |
| fast | thrpt | 1 | 10 | 107.895708 | 6.584674 | ops/s | 256 | 3.720950575 | 1.392453537 |
| fast | thrpt | 1 | 10 | 56.245336 | 2.729061 | ops/s | 320 | 3.170170846 | 1.417728592 |
| fast | thrpt | 1 | 10 | 32.917996 | 2.196624 | ops/s | 384 | 3.342125323 | 1.433783932 |
| fast | thrpt | 1 | 10 | 20.960189 | 2.077684 | ops/s | 448 | 3.328948087 | 1.449725854 |
| fast | thrpt | 1 | 10 | 14.005186 | 0.7839 | ops/s | 512 | 3.231390564 | 1.445957112 |
| fast | thrpt | 1 | 10 | 8.827584 | 0.883654 | ops/s | 576 | 3.091713481 | 1.297675056 |
| fast | thrpt | 1 | 10 | 7.455607 | 0.442882 | ops/s | 640 | 3.840605937 | 1.503417416 |
| fast | thrpt | 1 | 10 | 5.322894 | 0.464362 | ops/s | 704 | 3.519850554 | 1.428638807 |
| fast | thrpt | 1 | 10 | 4.308522 | 0.153846 | ops/s | 768 | 3.605919419 | 1.501303934 |
| fast | thrpt | 1 | 10 | 3.375274 | 0.106715 | ops/s | 832 | 3.474910097 | 1.495325228 |
| fast | thrpt | 1 | 10 | 2.320152 | 0.367881 | ops/s | 896 | 3.094703735 | 1.28379924 |
| fast | thrpt | 1 | 10 | 2.057478 | 0.150198 | ops/s | 960 | 3.533376381 | 1.400249889 |
| fast | thrpt | 1 | 10 | 1.66255 | 0.181116 | ops/s | 1024 | 4.180538513 | 1.3731919 |
Interestingly, the blocked algorithm is now the worst native JVM implementation. The code generated by C2 got a lot faster, but peaks at 1.5 flops/cycle, which still doesn’t compete with LMS. Why? Taking a look at the assembly, it’s clear that the autovectoriser choked on the array offsets and produced scalar SSE2 code, just like the implementations in the paper. I wasn’t expecting this.
vmovss xmm5,dword ptr [rdi+rcx*4+10h]
vfmadd231ss xmm5,xmm6,xmm2
vmovss dword ptr [rdi+rcx*4+10h],xmm5
Is this the end of the story? No, with some hacks and the cost of array allocation and a copy or two, autovectorisation can be tricked into working again to generate faster code:
public void fast(float[] a, float[] b, float[] c, int n) {
float[] bBuffer = new float[n];
float[] cBuffer = new float[n];
int in = 0;
for (int i = 0; i < n; ++i) {
int kn = 0;
for (int k = 0; k < n; ++k) {
float aik = a[in + k];
System.arraycopy(b, kn, bBuffer, 0, n);
saxpy(n, aik, bBuffer, cBuffer);
kn += n;
}
System.arraycopy(cBuffer, 0, c, in, n);
Arrays.fill(cBuffer, 0f);
in += n;
}
}
private void saxpy(int n, float aik, float[] b, float[] c) {
for (int i = 0; i < n; ++i) {
c[i] += aik * b[i];
}
}
Adding this hack into the NGen benchmark (back in JDK 1.8.0_131) I get closer to the LMS generated code, and beat it beyond L3 cache residency (6MB). LMS is still faster when both matrices fit in L3 concurrently, but by percentage points rather than a multiple. The cost of the hacky array buffers gives the game up for small matrices.
====================================================
Benchmarking MMM.jMMM.fast (JVM implementation)
----------------------------------------------------
Size (N) | Flops / Cycle
----------------------------------------------------
8 | 0.2500390686
32 | 0.7710872405
64 | 1.1302489072
128 | 2.5113453810
192 | 2.9525859816
256 | 3.1180920385
320 | 3.1081563593
384 | 3.1458423577
448 | 3.0493148252
512 | 3.0551158263
576 | 3.1430376938
640 | 3.2169923048
704 | 3.1026513283
768 | 2.4190053777
832 | 3.3358586705
896 | 3.0755689237
960 | 2.9996690697
1024 | 2.2935654309
====================================================
====================================================
Benchmarking MMM.nMMM.blocked (LMS generated)
----------------------------------------------------
Size (N) | Flops / Cycle
----------------------------------------------------
8 | 1.0001562744
32 | 5.3330416826
64 | 5.8180867784
128 | 5.1717318641
192 | 5.1639907462
256 | 4.3418618628
320 | 5.2536572701
384 | 4.0801359215
448 | 4.1337007093
512 | 3.2678160754
576 | 3.7973028890
640 | 3.3557513664
704 | 4.0103133240
768 | 3.4188362575
832 | 3.2189488327
896 | 3.2316685219
960 | 2.9985655539
1024 | 1.7750946796
====================================================
With the benchmark below I calculate flops/cycle with improved JDK10 autovectorisation.
@Benchmark
public void fastBuffered(Blackhole bh) {
fastBuffered(a, b, c, size);
bh.consume(c);
}
public void fastBuffered(float[] a, float[] b, float[] c, int n) {
float[] bBuffer = new float[n];
float[] cBuffer = new float[n];
int in = 0;
for (int i = 0; i < n; ++i) {
int kn = 0;
for (int k = 0; k < n; ++k) {
float aik = a[in + k];
System.arraycopy(b, kn, bBuffer, 0, n);
saxpy(n, aik, bBuffer, cBuffer);
kn += n;
}
System.arraycopy(cBuffer, 0, c, in, n);
Arrays.fill(cBuffer, 0f);
in += n;
}
}
private void saxpy(int n, float aik, float[] b, float[] c) {
for (int i = 0; i < n; ++i) {
c[i] = Math.fma(aik, b[i], c[i]);
}
}
Just as in the modified NGen benchmark, this starts paying off once the matrices have 64 rows and columns. Finally, and it took an upgrade and a hack, I breached 4 Flops per cycle:
| Benchmark | Mode | Threads | Samples | Score | Score Error (99.9%) | Unit | Param: size | Flops / Cycle |
|---|---|---|---|---|---|---|---|---|
| fastBuffered | thrpt | 1 | 10 | 1047184.034 | 63532.95095 | ops/s | 8 | 0.412429404 |
| fastBuffered | thrpt | 1 | 10 | 58373.56367 | 3239.615866 | ops/s | 32 | 1.471373026 |
| fastBuffered | thrpt | 1 | 10 | 12099.41654 | 497.33988 | ops/s | 64 | 2.439838038 |
| fastBuffered | thrpt | 1 | 10 | 2136.50264 | 105.038006 | ops/s | 128 | 3.446592911 |
| fastBuffered | thrpt | 1 | 10 | 673.470622 | 102.577237 | ops/s | 192 | 3.666730488 |
| fastBuffered | thrpt | 1 | 10 | 305.541519 | 25.959163 | ops/s | 256 | 3.943181586 |
| fastBuffered | thrpt | 1 | 10 | 158.437372 | 6.708384 | ops/s | 320 | 3.993596774 |
| fastBuffered | thrpt | 1 | 10 | 88.283718 | 7.58883 | ops/s | 384 | 3.845306266 |
| fastBuffered | thrpt | 1 | 10 | 58.574507 | 4.248521 | ops/s | 448 | 4.051345968 |
| fastBuffered | thrpt | 1 | 10 | 37.183635 | 4.360319 | ops/s | 512 | 3.839002314 |
| fastBuffered | thrpt | 1 | 10 | 29.949884 | 0.63346 | ops/s | 576 | 4.40270151 |
| fastBuffered | thrpt | 1 | 10 | 20.715833 | 4.175897 | ops/s | 640 | 4.177331789 |
| fastBuffered | thrpt | 1 | 10 | 10.824837 | 0.902983 | ops/s | 704 | 2.905333492 |
| fastBuffered | thrpt | 1 | 10 | 8.285254 | 1.438701 | ops/s | 768 | 2.886995686 |
| fastBuffered | thrpt | 1 | 10 | 6.17029 | 0.746537 | ops/s | 832 | 2.733582608 |
| fastBuffered | thrpt | 1 | 10 | 4.828872 | 1.316901 | ops/s | 896 | 2.671937962 |
| fastBuffered | thrpt | 1 | 10 | 3.6343 | 1.293923 | ops/s | 960 | 2.473381573 |
| fastBuffered | thrpt | 1 | 10 | 2.458296 | 0.171224 | ops/s | 1024 | 2.030442485 |
The code generated for the core of the loop looks better now:
vmovdqu ymm1,ymmword ptr [r13+r11*4+10h]
vfmadd231ps ymm1,ymm3,ymmword ptr [r14+r11*4+10h]
vmovdqu ymmword ptr [r13+r11*4+10h],ymm1
These benchmark results can be compared on a line chart.
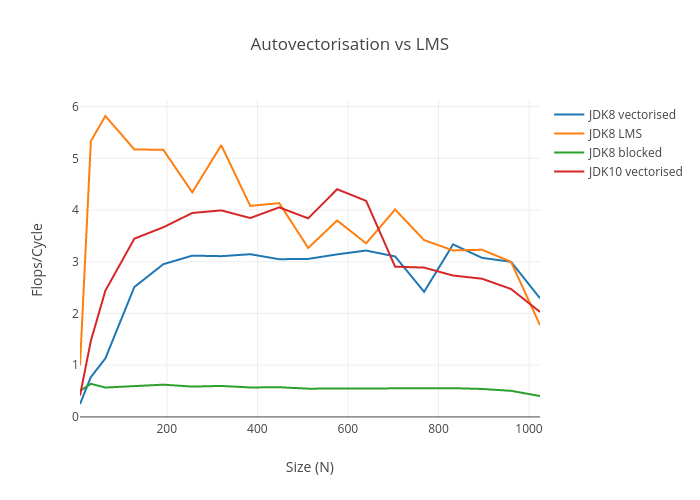
Given this improvement, it would be exciting to see how LMS can profit from JDK9 or JDK10 - does LMS provide the impetus to resume maintenance of scala-virtualized? L3 cache, which the LMS generated code seems to depend on for throughput, is typically shared between cores: a single thread rarely enjoys exclusive access. I would like to see benchmarks for the LMS generated code in the presence of concurrency.